问题 L: 方格取数
题目描述
输入格式
第一行有两个整数 n,m。
接下来 n 行每行 m 个整数,依次代表每个方格中的整数。
对于 100% 的数据,1≤n,m≤103 。方格中整数的绝对值不超过 104。
输出格式
样例1解释:
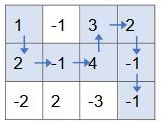
按上述走法,取到的数之和为1+2+(-1)+4+3+2+(-1)+(-1)=9,可以证明为最大值。
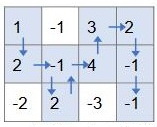
注意,上述走法是错误的,因为第2行第2列的方格走过了两次,而根据题意,不能重复经过已经走过的方格。
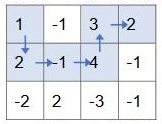
另外,上述走法也是错误的,因为没有右下角的终点。
输入样例2:
2 5 -1 -1 -3 -2 -7 -2 -1 -4 -1 -2
输出样例2:
-10
样例1解释:

按上述走法,取到的数之和为(-1)+(-1)+(-3)+(-2)+(-1)+(-2)=-10,可以证明为最大值。因此,请注意,取到的数之和的最大值也可能是负数。
数据规模与约定
对于 20% 的数据,n,m≤5。
对于 40% 的数据,n,m≤500。
对于 70% 的数据,n,m≤300。
对于 100% 的数据,1≤n,m≤103 。方格中整数的绝对值不超过 104。
输入样例 复制
3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1输出样例 复制
9数据范围与提示
样例1解释:

按上述走法,取到的数之和为1+2+(-1)+4+3+2+(-1)+(-1)=9,可以证明为最大值。

注意,上述走法是错误的,因为第2行第2列的方格走过了两次,而根据题意,不能重复经过已经走过的方格。

另外,上述走法也是错误的,因为没有右下角的终点。
输入样例2:
2 5 -1 -1 -3 -2 -7 -2 -1 -4 -1 -2
输出样例2:
-10
样例1解释:

按上述走法,取到的数之和为(-1)+(-1)+(-3)+(-2)+(-1)+(-2)=-10,可以证明为最大值。因此,请注意,取到的数之和的最大值也可能是负数。
数据规模与约定
对于 20% 的数据,n,m≤5。
对于 40% 的数据,n,m≤500。
对于 70% 的数据,n,m≤300。
对于 100% 的数据,1≤n,m≤103 。方格中整数的绝对值不超过 104。