问题 A: Almost Acyclic
题目描述
We call a connected undirected graph almost-acyclic, if the graph has no cycles, or all the simple cycles in it share at least one common point.
You are given a complete undirected graph �=(�,�)G=(V,E) with �n vertices. Each edge (�,�)(i,j) has a weight ��,�wi,j. Calculate (�(�)f(G) is 11 if �G is almost-acyclic, or 00 otherwise):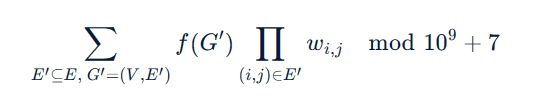
输入格式
The first line contains a single integer �T (1≤�≤161≤T≤16), denoting the number of test cases.
For each test case, the first line contains an integer �n (1≤�≤161≤n≤16).
The next �n lines each contains �n integers. The �j-th number in the �i-th line denotes ��,�wi,j (0≤��,�<109+70≤wi,j<109+7).
It is guaranteed that ��,�=��,�wi,j=wj,i, ��,�=0wi,i=0.
It is guaranteed that for each 1≤�≤161≤i≤16, there is at most one test case satisfying �=�n=i.
输出格式
输入样例 复制
2
3
0 1 2
1 0 1
2 1 0
5
0 1 0 1 1
1 0 1 1 1
0 1 0 1 0
1 1 1 0 1
1 1 0 1 0输出样例 复制
7
120