问题 H: Bracelet Crossings
题目描述
- 每个手链是一个简单闭合折线——一组顶点(点)依次用线段连接,并且第一个点和最后一个点相同(欢迎查阅维基百科页面了解更多详情:[Polygonal_chain](https://en.wikipedia.org/wiki/Polygonal_chain),或百度百科:[折线](https://baike.baidu.com/item/%E6%8A%98%E7%BA%BF/486302)),
- 没有手链与自身相交(这对应「简单」折线);
- 以及没有两条手链相交。
不幸的是,就在 Bessie 如此小心翼翼地布置好手链之后,Farmer John 开着拖拉机经过,桌子晃动起来,导致手链四处移动甚至可能断成了多个(不一定是闭合的或简单的)折线!在那之后,Bessie 还是想检查以上三个条件是否仍然成立。然而,天色已暗,她现在无法看清手链。
幸好 Bessie 有一个手电筒。她选择了 $M$($1\le M\le 50$)条垂直线 $x=1, x=2, \ldots, x=M$,并且对于每条线,她用手电筒的光沿着那条线从 $y=-\infty$ 扫至 $y=\infty$,按照出现的顺序记录她看到的所有手链的颜色。幸运的是,没有光束穿过任何折线的顶点或同时穿过两条线段。此外,对于每一束光,所有出现的颜色都恰好出现了两次。
你能帮助 Bessie 使用此信息来确定手链是否仍然满足上述所有三个条件吗?
## 输入格式
每个测试用例的输入包含 $T$ 个子测试用例($1 \leq T \leq 50$),所有子测试用例必须全部回答正确才能通过整个测试用例。相邻的子测试用例之间用空行分隔。
输入的第一行包含 $T$。之后是 $T$ 个子测试用例。
每个子测试用例的第一行包含两个整数 $N$ 和 $M$。此后每个子测试用例还包含 $M$ 行。对 $1$ 到 $M$ 的每一个 $i$,第 $i$ 行包含一个整数 $k_i$($0\le k_i\le 2N$,$k_i$ 为偶数),然后是 $k_i$ 个整数 $c_{i1}, c_{i2},\ldots, c_{ik_i}$($c_{ij}\in [1,N]$,每个 $c_{ij}$ 出现零次或两次)。这表示当 Bessie 将手电筒从 $(i,-\infty)$ 扫至 $(i,\infty)$ 时,她按顺序 $c_{i1}, c_{i2},\ldots, c_{ik_i}$ 看到了这些颜色。
## 输出格式
对每个子测试用例,如果有可能使得以上三个条件均满足则输出 YES。否则,输出 NO。
【数据范围】
- 测试点 2 满足 $N = 1$。
- 测试点 3-5 满足 $N=2$。
- 测试点 6-8 满足 $M=1$。
- 测试点 9-14 满足 $M=2$。
- 测试点 15-20 没有额外限制。
Bessie the cow enjoys arts and crafts. In her free time, she has made N (1≤N≤50) bracelets, conveniently numbered 1…N. The ith bracelet is painted color ii out of a set of N different colors. After constructing the bracelets, Bessie placed them on a table for display (which we can think of as the 2D plane). She was careful to arrange the bracelets to satisfy the following three conditions:
- Every bracelet was a single closed polygonal chain -- a series of vertices (points) connected sequentially by line segments, where the first and last points are the same (Feel welcome to consult the wikipedia page for more detail: polygonal chain),
- No bracelet intersected itself (this corresponds to a "simple" polygonal chain); and
- No two bracelets intersected.
Unfortunately, right after Bessie arranged the bracelets in such a careful manner, Farmer John drove by in his tractor, shaking the table and causing the bracelets to shift around and possibly break into multiple (not necessarily closed or simple) polygonal chains! Afterward, Bessie wanted to check whether the three conditions above still held. However, it was dark, so she couldn't see the bracelets anymore.
Fortunately, Bessie had a flashlight. She chose MM (1≤M≤50) vertical lines x=1,x=2,…,x=M and for each line, she swept the beam of the flashlight along that line from y=−∞ to y=∞, recording the colors of all bracelets she saw in the order they appeared. Luckily, no beam crossed over any vertex of any polygonal chain or two line segments at the same time. Furthermore, for each beam, every color that appeared appeared exactly twice.
Can you help Bessie use this information to determine whether it is possible that the bracelets still satisfy all three of the conditions above?
输入格式
The first line of the input contains T. Each of the T sub-test cases then follow.
The first line of each sub-test case contains two integers N and MM. Each sub-test case then contains MM additional lines. For each ii from 11 to MM, the i-th additional line contains an integer ki (0≤ki≤2N, ki even), followed by ki integers ci1,ci2,…,ciki (cij∈[1,N], every cij appears zero or two times). This means that when Bessie swept her flashlight from (i,−∞) to (i,∞), she encountered the colors ci1,ci2,…,ciki in that order.
输出格式
输入样例 复制
5
1 2
2 1 1
2 1 1
1 3
2 1 1
0
2 1 1
2 1
4 1 2 1 2
4 2
6 1 2 2 3 3 1
6 1 2 4 4 2 1
2 2
4 1 1 2 2
4 2 2 1 1输出样例 复制
YES
NO
NO
YES
NO数据范围与提示
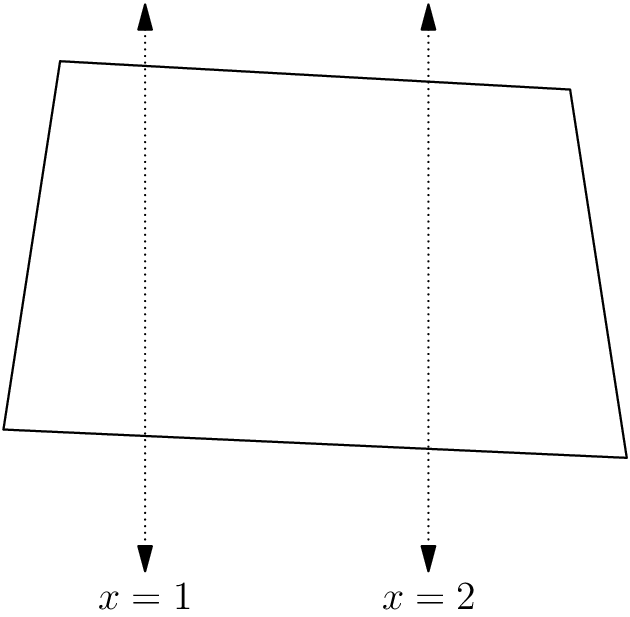
An example of a feasible bracelet configuration for the first sub-case is:
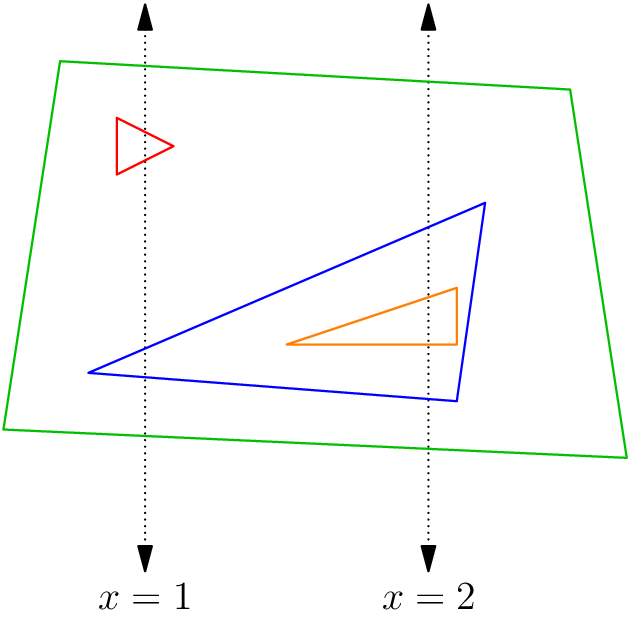
For the fourth sub-case, a feasible arrangement is the following:
SCORING:
- Test case 2 satisfies N=1N=1.
- Test cases 3-5 satisfy N=2N=2.
- Test cases 6-8 satisfy M=1M=1.
- Test cases 9-14 satisfy M=2M=2.
- Test cases 15-20 satisfy no additional constraints.