问题 G: 量子弹弓

帝国控制着 $n$ 个脉冲星系，编号为 $1,2,3,\cdots ,n$，并给每个星系中安装了一个 量子弹弓，编号为 $i$（$1\le i\le n$）的星系中的量子弹弓强度为非负整数 pipi。为了增强星系之间的联络，总督希望用 $n-1$ 条 虫洞通道 连接这些星系使得它们连通（其中每条虫洞通道的两端连接两个星系），也就是形成一棵树的结构。

量子弹弓可以让飞船由宇宙空间从一个星系穿梭到另一个星系，但有一个重要的前提。具体地，处在编号为 $i$（$1\le i\le n$）的星系中的量子弹弓可以让飞船从该星系 穿梭 到编号为 $j$（$1\le j\le n$，$i\ne j$）的星系，当且仅当在这两个星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量不超过这个量子弹弓的强度。

总督现在要求你制定星系间交通联络的方案。你需要构造这样一种建立虫洞通道的方式，和星系间的一个包含每个星系恰好一次的回路，使得飞船从回路上的任意一个星系开始，都能一直穿梭到回路中当前所处星系的后一个星系，最终回到初始所在星系。

由于总督下午就要去参加听证会，他只希望知道是否存在这样的构造。

形式化地，你需要判断是否存在一棵由编号为 $1,2,3,\cdots ,n$ 的点构成的树 $T$ 和一个 $[1,n]$ 的排列 $a$，使得对于所有整数 $i$（$1\le i\le n$），dis(ai,a(imodn)+1)≤paidis(ai,a(imodn)+1)≤pai，其中 $\text{dis}(u,v)$ 表示编号为 $u,v$ 的两点在 $T$ 上的唯一简单路径的边数，$\mathrm{mod}$ 表示取模，例如 $3\mathrm{mod}2=1,(-7)\mathrm{mod}3=2$。

本题包含多组测试数据。

首先在第一行输入一个整数 $T$（1≤T≤1061≤T≤106）表示测试数据组数。

对于每一组测试数据，输入包含两行。

第一行包含一个整数 $n$（2≤n≤105,2≤∑n≤1062≤n≤105,2≤∑n≤106），表示脉冲星系数量。

第二行包含 $n$ 个整数 p1,p2,p3,⋯,pnp1,p2,p3,⋯,pn（0≤p1,p2,p3,⋯,pn<n0≤p1,p2,p3,⋯,pn<n）表示每个星系中量子弹弓的强度。

对于每一组测试数据，输出包含一行。

若不存在满足题意的建立虫洞通道的方式与星系间的一个回路，输出一行包含一个字符串 NO。若存在，输出一行包含一个字符串 YES。

这个样例共有五组测试数据。

在第一组测试数据中，可以构造以下的建立虫洞通道的方式以及星系回路 $a=[1,2,3,4]$。

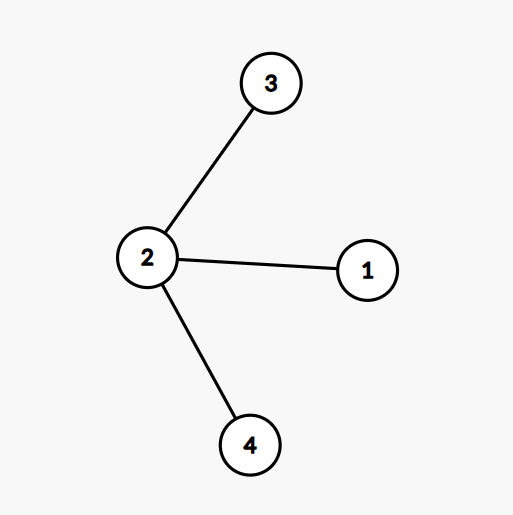
此时：

1. 编号为 a1=1,a2=2a1=1,a2=2 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa1=21≤pa1=2。
2. 编号为 a2=2,a3=3a2=2,a3=3 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa2=11≤pa2=1。
3. 编号为 a3=3,a4=4a3=3,a4=4 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $2$，2≤pa3=22≤pa3=2。
4. 编号为 a4=4,a1=1a4=4,a1=1 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $2$，2≤pa4=22≤pa4=2。

在第二组测试数据中，可以构造以下的建立虫洞通道的方式以及星系回路 $a=[2,3,4,5,1]$。

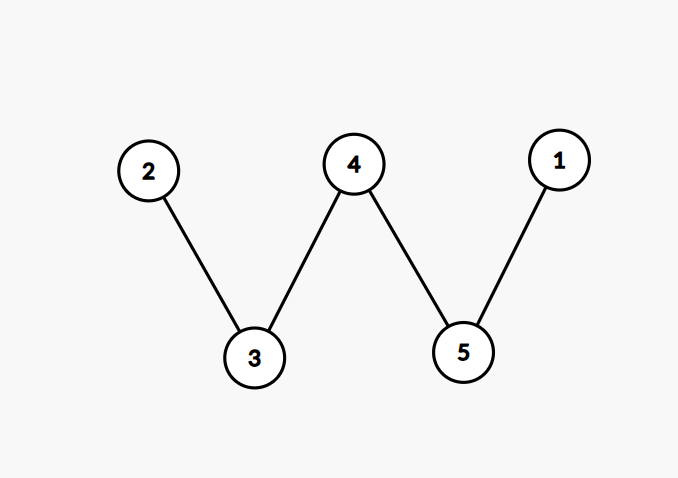
此时：

1. 编号为 a1=2,a2=3a1=2,a2=3 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa1=11≤pa1=1。
2. 编号为 a2=3,a3=4a2=3,a3=4 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa2=11≤pa2=1。
3. 编号为 a3=4,a4=5a3=4,a4=5 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa3=11≤pa3=1。
4. 编号为 a4=5,a5=1a4=5,a5=1 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $1$，1≤pa4=11≤pa4=1。
5. 编号为 a5=1,a1=2a5=1,a1=2 的星系之间由虫洞通道构成的唯一简单路径中，虫洞通道的数量为 $4$，4≤pa5=44≤pa5=4。

可以证明，在第三、四组测试数据中，不存在满足题意的建立虫洞通道的方式与星系间的一个回路；在第五组测试数据中，存在满足题意的建立虫洞通道的方式与星系间的一个回路。