问题 I: 统计强连通

给定一张 简单有向图 $G$ 包含编号为 $1,2,3,\cdots ,n$ 的点。此图包含 $m$ 条边，编号为 $1,2,3,\cdots ,m$，其中第 $i$（$1\le i\le m$）条边为 ui→viui→vi。

定义有向图 G0G0 是一张包含两个编号分别为 $1,2$ 的点与一条边 $1\to 2$ 的图。对于整数 $k$（$k\ge 1$），定义有向图 GkGk 是将 Gk−1Gk−1 中的每一条边使用 $G$ 同时替换所得到的图（可见 样例解释 中的参考图）。替换时将 Gk−1Gk−1 中的每一条边的起点视为 $G$ 中编号为 $1$ 的点，终点视为 $G$ 中编号为 $2$ 的点。

具体地，对于正整数 $k$，按下面的方式构造有向图 GkGk：

1. 首先使 GkGk 中包含与 Gk−1Gk−1 相同数目的点，并给它们分配与 Gk−1Gk−1 相同的编号。此时 GkGk 中不包含任何边。
2. 对于 Gk−1Gk−1 中的每条有向边，轮流执行一次添加操作。
3. 给 GkGk 中的点重新分配连续正整数编号。

一次对 Gk−1Gk−1 中的有向边 $u\to v$ 的添加操作如下：

1. 在 GkGk 中加入 $n$ 个新点，并按照图 $G$ 的方式在这 $n$ 个新点之间连接 $m$ 条有向边。设这 $n$ 个新点中，与图 $G$ 中编号为 $1,2$ 的点对应的点的编号分别是 $x,y$。
2. 在 GkGk 中找到编号为 $u,v$ 的点。合并编号为 $u,x$ 的点、编号为 $v,y$ 的点。合并编号为 $a,b$ 的点时，把所有形如 $b\to \gamma$ 的边修改为 $a\to \gamma$，把所有形如 $\gamma \to b$ 的边修改为 $\gamma \to a$。由于不可能出现 $a\to b$ 与 $b\to a$，所以不需要考虑。允许出现重边。

如果你还是不理解这个过程，可以参考 样例解释 的伪代码。

给定图 $G$ 和非负整数 k′k′，计算 Gk′Gk′ 中的强连通分量的个数。对 $1000000007$ 取模。

本题包含多组测试数据。

首先在第一行输入一个整数 $T$（$1\le T\le 100$）表示测试数据组数。

对于每一组测试数据，输入包含 $m+1$ 行。

第一行包含三个整数 n,m,k′n,m,k′（2≤n≤1052≤n≤105，2≤∑n≤3×1052≤∑n≤3×105，0≤m≤∑m≤1060≤m≤∑m≤106，0≤k′≤10180≤k′≤1018），分别表示 $G$ 中点与边的数量，以及与计算答案有关的参数。

接下来 $m$ 行，第 $i+1$（$1\le i\le m$）行包含两个整数 ui,viui,vi（1≤ui,vi≤n1≤ui,vi≤n）表示一条 $G$ 中的边 ui→viui→vi。

保证输入的点与边构成一张简单有向图。（即无重边与自环）

在样例的第二组测试数据中，将 G1G1 中的每一条边使用 $G$ 同时替换的过程如下图所示（其中黑色虚线边表示 G1G1 中的边 u′→v′u′→v′，这条边仅作指示作用，在 G2G2 中不存在，仅一部分图中绘制了黑色虚线边）：

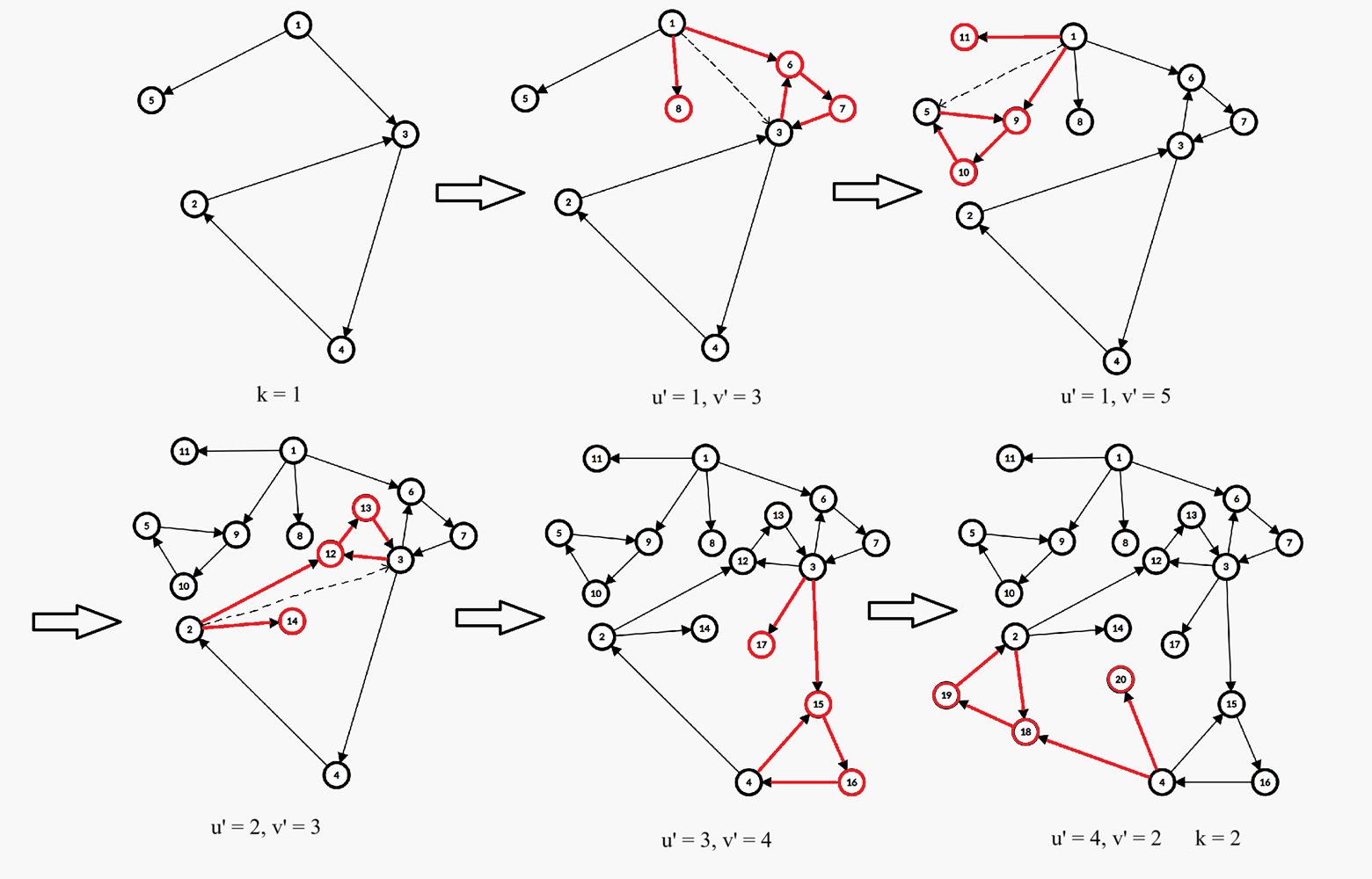
答案为 $8$。

在这里给出伪代码，伪代码以图 $G$ 和整数 $k$ 作为输入，返回图 GkGk：