问题 J: 海上的太阳

从前有一座山，山的一侧是海，海上有个太阳。

在平面直角坐标系中，山坡 的形状可以用一个定义域是 $[0,+\infty )$ 的 非负整系数 多项式函数 y=amxm+am−1xm−1+⋯+a1xy=amxm+am−1xm−1+⋯+a1x 表示。太阳 的横坐标是 $X$，纵坐标是 $Y$。可以认为山坡向无穷远处延伸，并且太阳不会移动。

有一天，房地产商想要在这条山坡上建造 $n$ 座 大楼。第 $i$（$1\le i\le n$）座大楼的高度为 hihi，并居住着 wiwi 个居民。大楼的宽度忽略不计。

出于很显然的原因，大楼必须保持竖直，并且底部必须要位于山坡上。大楼之间的顺序可以任意排列。不过，房地产商还有一些要求：

1. 大楼之间需要保持一定的距离。具体地，任意两座大楼的底部的欧几里得距离必须要大于等于它们的高度的较大值。
2. 大楼需要保证采光。具体地，任意一座大楼上的任意一点与太阳的连线不能穿过其它大楼（但可以恰好经过其它大楼的端点）。

由于山坡的右边是无限延伸的，这里的居民必须要向左走前往外地。

在原点处有一个 码头。居民们必须要从他们所处的大楼的底部出发，沿着山坡走到码头才能离开。但是居民们都不喜欢走路。因此，对于第 $i$（$1\le i\le n$）座大楼，这里的居民产生的不满意度是 wi×disiwi×disi，其中 disidisi 表示从第 $i$ 座大楼底部 沿着山坡 走到码头的距离。一个建造方案的不满意度就是所有大楼的不满意度之和。

现在，请求出在所有满足要求的大楼建造方案中，不满意度最小的方案，并输出这个不满意度。保证答案处于实数集合 {0}∪[10−9,1010){0}∪[10−9,1010) 中。

本题包含多组测试数据。

首先在第一行输入一个整数 $T$（$1\le T\le 100$）表示测试数据组数。

对于每一组测试数据，输入包含 $n+2$ 行。

第一行包含四个整数 $n,m,X,Y$（$1\le n\le 6$，$1\le m\le 5$，−105≤X≤−1−105≤X≤−1，2≤Y≤1052≤Y≤105），分别表示大楼的数量，山坡多项式函数的次数和太阳的横坐标与纵坐标。

第二行包含 $m$ 个整数 a1,a2,a3,⋯,ama1,a2,a3,⋯,am（0≤a1,a2,⋯,am−1≤1000≤a1,a2,⋯,am−1≤100，1≤am≤1001≤am≤100）分别表示山坡多项式函数的各个系数。

接下来 $n$ 行，第 $i+2$（$1\le i\le n$）行包含两个整数 hi,wihi,wi（1≤hi<Y1≤hi<Y，1≤wi≤1001≤wi≤100），分别表示第 $i$ 座大楼的高度和居民数。

保证满足 $n>3$ 的测试数据不超过五组。

对于每组测试数据，输出一行一个浮点数，表示不满意度的最小值。

请使用科学计数法输出答案，并保留四位小数。

具体地，根据题目的限制，如果答案为正实数，那么可以唯一表示为 a×10ka×10k 的形式，其中 $1\le a<10$，$k$ 是整数，且 $-9\le k\le 9$。此时需要输出 x.xxxxe+x 或 x.xxxxe-x，其中：

1. 前面的五个 x 表示 $a$ 保留四位小数的值，不足的数位补 0。
2. 后面的一个 x 表示 $k$ 的绝对值。
3. 中间的 + 或 - 符号表示 $k$ 的符号。特别地，如果 $k=0$，输出 + 号。

如果答案为 $0$，那么输出 0.0000e+0。

使用 C++ 语言参加竞赛的选手请注意：由于某些问题，不保证编译器自带的输出语句一定按照本题中的格式输出浮点数。如有需要，请自行实现输出函数。在 输出格式 的最后提供了一份 C++ 代码，供参考。

使用 Java 语言参加竞赛的选手请注意：由于某些问题，不保证编译器自带的输出语句一定按照本题中的格式输出浮点数。如有需要，请自行实现输出函数。

下面的 C++ 代码实现了一个按照题目要求输出满足 d∈{0}∪[10−9,1010)d∈{0}∪[10−9,1010) 的实数 $d$ 的函数。

void output(long double x){
    static char s[25];
    sprintf(s,"%.4Le",x);
    for(int i:{0,1,2,3,4,5,6,7}) printf("%c",s[i]);
    printf("%c",s[strlen(s)-1]);
}

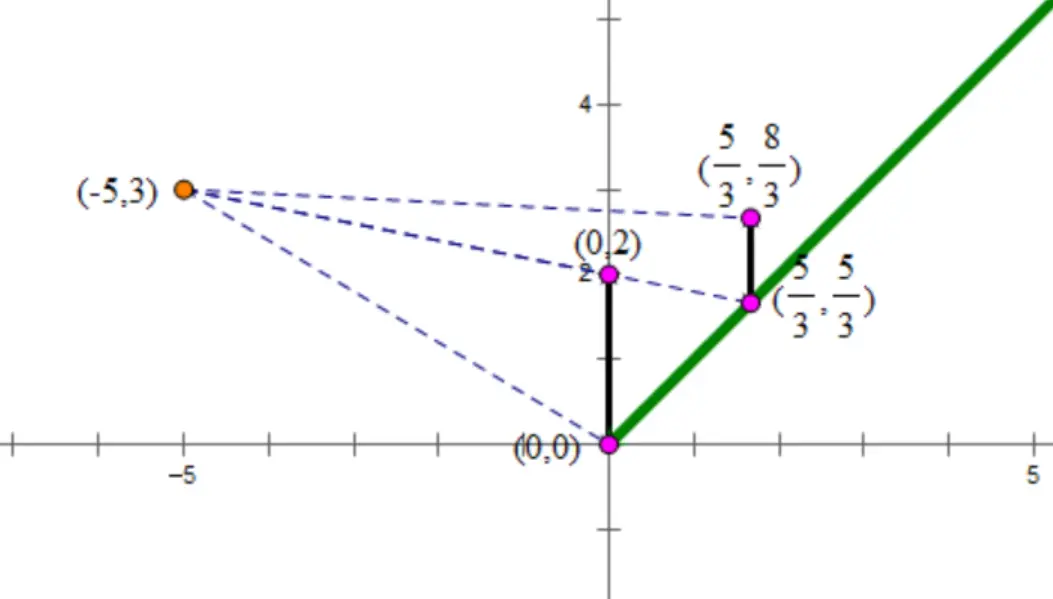
在样例的第一组测试数据中，太阳的横坐标 $X=-5$，纵坐标 $Y=3$，如图橙色点所示。山坡的形状是函数 $y=x$，如图绿色射线所示。

此时，最优的方案是将第一座大楼建在 x=53x=35 的位置，第二座大楼建在 $x=0$ 的位置，如图黑色线段所示。不满意度是 523352，大约是 $2.3570226040$。因此输出 2.3570e+0。