2520: 机场登机口调整模拟
题目描述
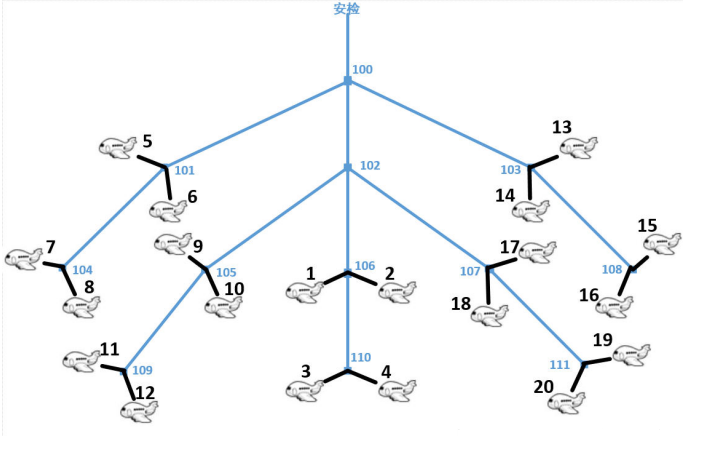
假设某机场所有登机口(Gate)呈树形排列(树的度为 3),安检处为树的根,如下图所示。
图中的分叉结点(编号大于等于 100)表示分叉路口,登机口用小于 00 的编号表示(其一定是一个叶结点)。
通过对机场所有出发航班的日志分析,得知每个登机口每天的平均发送旅客流量。
作为提升机场服务水平的一个措施,在不改变所有航班相对关系的情况下(即:出发时间不变,原在同一登机口的航班不变),仅改变登机口(例如:将 3 号登机口改到 5 号登机口的位置),使得整体旅客到登机口的时间有所减少(即:从安检口到登机口所经过的分叉路口最少)。
编写程序模拟上述登机口的调整,登机口调整规则如下:
- 首先按照由大到小的顺序对输入的登机口流量进行排序,流量相同的按照登机口编号由小到大排序;
- 从上述登机口树的树根开始,按照从上到下(安检口在最上方)、从左到右的顺序,依次放置上面排序后的登机口。
例如上图的树中,若只考虑登机口,则从上到下有三层,
第一层从左到右的顺序为: 5、6、14、13,
第二层从左到右的顺序为: 7、8、9、10、1、2、18、17、16、15,
第三层从左到右的顺序为:1、12、3、4、20、19。
若按规则 1 排序后流量由大至小的前五个登机口为3、12、16、20、15,则将流量最大的 3 号登机口调整到最上层且最左边的位置(即: 5 号登机口的位置), 12 号调整到 6 号,16 号调整到 14 号,20 号调整到 13 号,15 号调整到第二层最左边的位置(即 7 号登机口的位置)。
输入格式
首先输入一个整数表示树结点关系的条目数。
接着在下一行开始,按层次从根开始依次输入树结点之间的关系。其中分叉结点编号从数字 100 开始(树根结点编号为 100,其它分叉结点编号没有规律但不会重复),登机口为编号小于 100 的数字(编号没有规律但不会重复,其一定是一个叶结点)。
树中结点间关系用下面方式描述:
R S1 S2 S3
其中 RR 为分叉结点,从左至右 S1,S2,S3 分别为树叉 RR 的子结点,其可为树叉或登机口,由于树的度为 3, S1,S2,S3 中至多可以 2 个为空,该项为空时用 -1 表示。
如:
100 101 102 103
表明编号 100 的树根有三个子叉,编号分别为 101、 102 和 103。
又如:
104 7 8 -1
表明树叉 104 上有 2 个编号分别为 7 和 8 的登机口。
假设分叉结点数不超过 100 个。
分叉结点输入的顺序不确定,但可以确定:输入某个分叉结点信息时,其父结点的信息已经输入。
在输入完树结点关系后,接下来输入登机口的流量信息,每个登机口流量信息分占一行,分别包括登机口编号( 1∼99 之间的整数)和流量(大于 0 的整数),两整数间以一个空格分隔。
输出格式
按照上述调整规则中排序后的顺序(即按旅客流量由大到小,流量相同的按照登机口编号由小到大)依次分行输出每个登机口的调整结果:先输出调整前的登机口编号,再输出要调整到的登机口编号。编号间均以一个空格分隔。
数据范围
分叉结点数量 [1,100],
分叉结点编号不超过 300。
登机口数量 [1,99],
流量数据范围 [1,10000]
输入样例 复制
12
100 101 102 103
103 14 108 13
101 5 104 6
104 7 8 -1
102 105 106 107
106 1 110 2
108 16 15 -1
107 18 111 17
110 3 4 -1
105 9 109 10
111 20 19 -1
109 11 12 -1
17 865
5 668
20 3000
13 1020
11 980
8 2202
15 1897
6 1001
14 922
7 2178
19 2189
1 1267
12 3281
2 980
18 1020
10 980
3 1876
9 1197
16 980
4 576输出样例 复制
12 5
20 6
8 14
19 13
7 7
15 8
3 9
1 10
9 1
13 2
18 18
6 17
2 16
10 15
11 11
16 12
14 3
17 4
5 20
4 19数据范围与提示
样例解释
样例输入了 12 条树结点关系,形成了如上图的树。
然后输入了 20 个登机口的流量,将这 20 个登机口按照上述调整规则 1 排序后形成的顺序为:12、20、8、19、7、15、3、1、9、13、18、6、2、10、11、16、14、17、5、4。
最后按该顺序将所有登机口按照上述调整规则 2 进行调整,输出调整结果。