3489: 学画画导致的
内存限制:524 MB
时间限制:4 S
题面:传统
评测方式:文本比较
上传者:
提交:35
通过:11
题目描述
现有 nn 行的三角形网格(下图展示了 n=2 的情形)和 3n 只颜色互不相同的刷子,颜色依次为 1,2,…,3n。每只刷子都有固定初始位置和运动方向,其中初始位置和运动方向如下方左图所示。
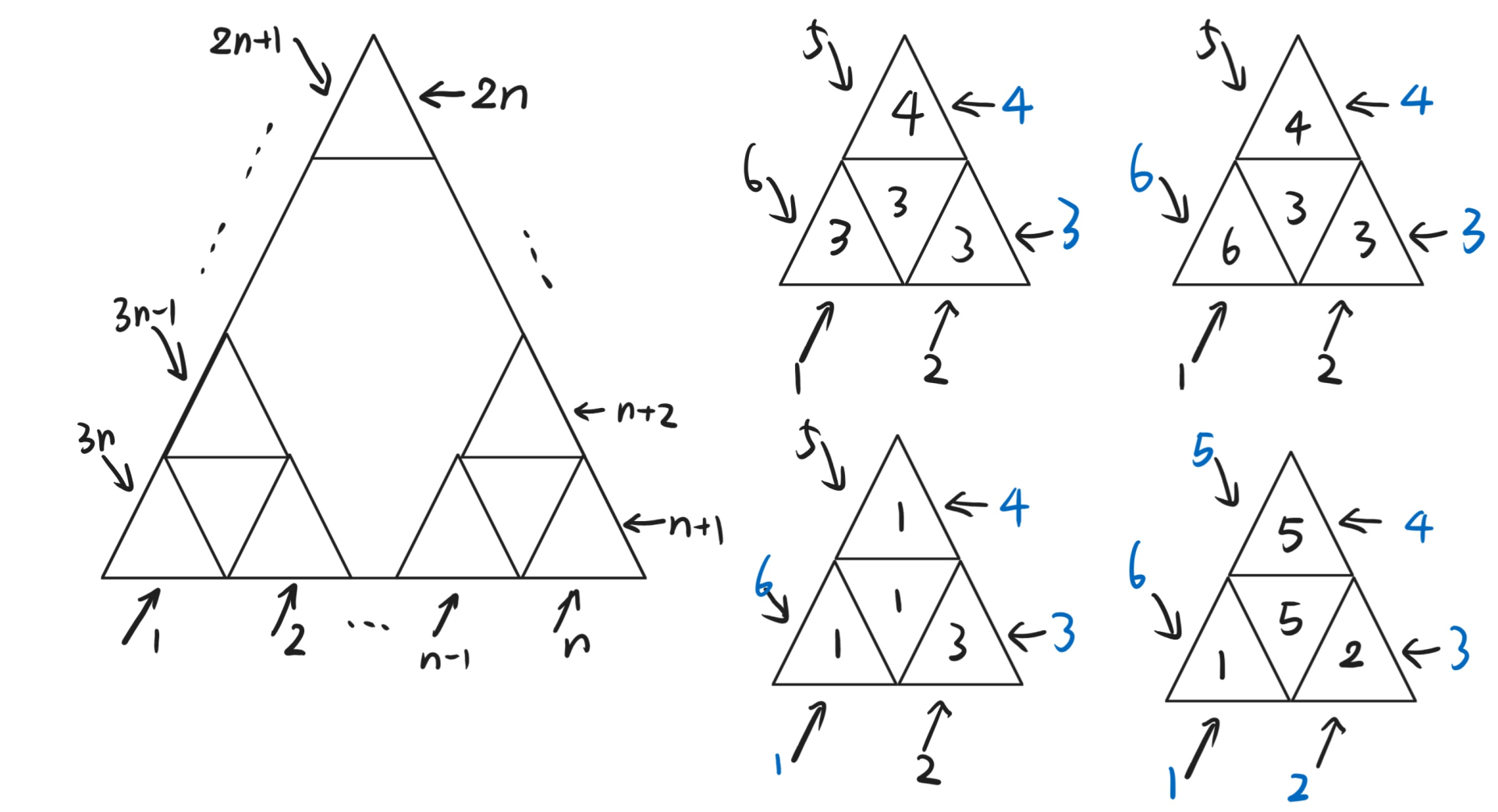
下面 yummy 将以某种顺序让每种刷子作用恰好一次。对于一个格子,其显示的颜色一定是最后一个经过它的刷子的颜色(也就是刷子会完全覆盖原来的颜色)。
给出一部分(m 个,可能重复)格子的最终颜色,判断是否存在符合题意的刷子作用顺序。
输入格式
本题有多组测试数据。输入的第一行有一个正整数 T(1≤T≤105)
对于每组数据:
第一行会给出两个正整数 n,m(1≤n,m≤3×105),表示三角形网格行数和已知颜色的格子数量。
之后 m 行,每行有三个数 x,y,col(1≤x≤n,1≤y≤2x−1,1≤col≤3n),表示“第 x 行的第 y个格子颜色为 col”。不保证 (x,y) 两两不同。
对于所有测试点,保证所有测试数据的 n 之和不超过 10e6,所有测试数据的 m 之和不超过 10e6。
输出格式
对于每组数据,输出一行一个字符串 Yes 或 No,表示符合题意的刷子作用顺序存在或不存在。
输入样例 复制
2
2 4
2 2 5
2 1 1
2 3 2
1 1 5
2 4
2 2 3
2 1 1
2 3 2
1 1 5输出样例 复制
Yes
No数据范围与提示
【样例解释】
对于第一组测试数据,考虑 3→4→6→1→5→2 的顺序,具体图示参见上方右图。
对于第二组测试数据,不难验证无论以何种方式操作都无法完成。