5356: 猜猜你的出路!
内存限制:256 MB
时间限制:2 S
题面:传统
评测方式:文本比较
上传者:
提交:10
通过:6
题目描述
阿姆尔买了一款新的电子游戏《猜猜你的出路!》。游戏的目标是从迷宫中找到一个看起来像高度为h的完美二叉树的出口。玩家最初站在树的根部,而树的出口位于某个叶子节点。
让我们从左到右索引从1到2h的所有叶节点。出口位于某个节点n,其中1≤n≤2h,玩家不知道出口在哪里,因此他必须猜测自己的出路!
Amr遵循简单的算法来选择路径。让我们考虑无限命令字符串“LRLRLRLRL…”(由交替字符“L”和“R”组成)。Amr使用以下规则顺序执行字符串的字符:
字符'L'表示“转到当前节点的左侧子节点”;
字符“R”表示“转到当前节点的右侧子节点”;
如果目标节点已经被访问,Amr将跳过当前命令,否则他将移动到目标节点;
如果Amr跳过了两个连续的命令,他会在执行下一个命令之前返回到当前节点的父节点;
如果他到达了不是出口的子节点,他将返回到当前节点的父节点;
如果他到达出口,游戏就结束了。
现在Amr想知道,如果他遵循这个算法,他在到达出口之前要访问多少节点?
Amr bought a new video game "Guess Your Way Out!". The goal of the game is to find an exit from the maze that looks like a perfect binary tree of height h. The player is initially standing at the root of the tree and the exit from the tree is located at some leaf node.
Let's index all the leaf nodes from the left to the right from 1 to 2h. The exit is located at some node n where 1≤n≤2h, the player doesn't know where the exit is so he has to guess his way out!
Amr follows simple algorithm to choose the path. Let's consider infinite command string "LRLRLRLRL..." (consisting of alternating characters 'L' and 'R'). Amr sequentially executes the characters of the string using following rules:
Let's index all the leaf nodes from the left to the right from 1 to 2h. The exit is located at some node n where 1≤n≤2h, the pla
Amr follows simple algorithm to choose the path. Let's consider infinite command string "LRLRLRLRL..." (consisting of alternating characters 'L' and 'R'). Amr sequentially executes the characters of the string using following rules:
- Character 'L' means "go to the left child of the current node";
- Character 'R' means "go to the right child of the current node";
- If the destination node is already visited, Amr skips current command, otherwise he moves to the destination node;
- If Amr skipped two consecutive commands, he goes back to the parent of the current node before executing next command;
- If he reached a leaf node that is not the exit, he returns to the parent of the current node;
- If he reaches an exit, the game is finished.
Input
Input consists of two integers h,n (1≤h≤50, 1≤n≤2h).
Output
Output a single integer representing the number of nodes (excluding the exit node) Amr is going to visit before reaching the exit by following this algorithm.
Examples
Input
1 2
Output
2
Input
2 3
Output
5
Input
3 6
Output
10
Input
10 1024
Output
2046
Note
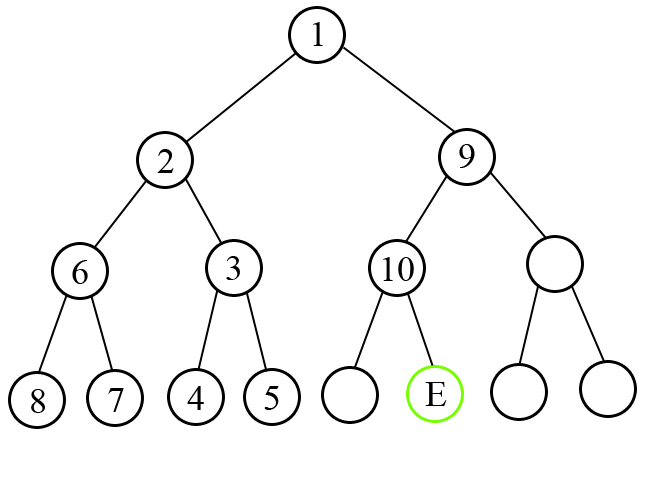
A perfect binary tree of height h is a binary tree consisting of h+1 levels. Level 0 consists of a single node called root, level h consists of 2h nodes called leaves. Each node that is not a leaf has exactly two children, left and right one. Following picture illustrates the sample test number 3. Nodes are labeled according to the order of visit.
输入格式
输入由两个整数h,n(1≤h≤50,1≤n≤2h)组成。
输出格式
输出一个整数,表示Amr在到达出口之前要访问的节点数(不包括出口节点)。
Input
1 2
Output
2
Input
2 3
Output
5
Input
3 6
Output
10
Input
10 1024
Output
2046
注意
高度为h的完美二叉树是由h+1级组成的二叉树。级别0由称为根的单个节点组成,级别h由称为叶的2h节点组成。每个不是叶子的节点正好有两个子节点,左一个和右一个。
下图显示了样本测试编号3。节点根据访问顺序进行标记。
输入样例 复制
1 2输出样例 复制
2数据范围与提示