7483: Boring Game
内存限制:128 MB
时间限制:1 S
题面:传统
评测方式:文本比较
上传者:
提交:36
通过:8
题目描述
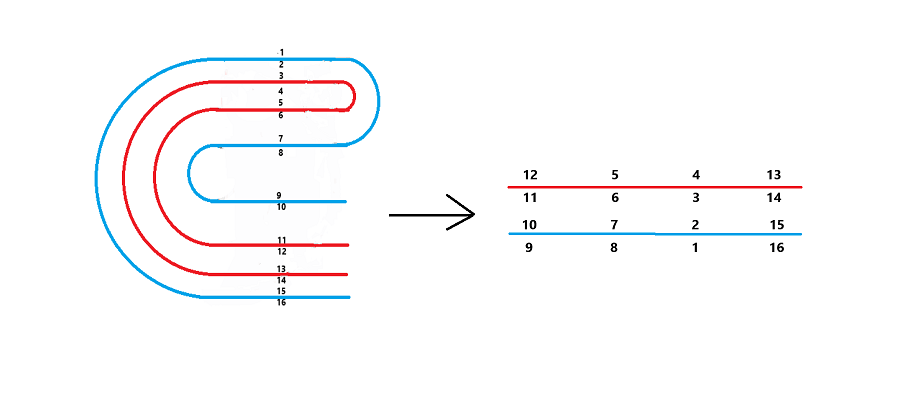
Given n sheets of paper, place them on the table in pile and fold them in half k times from left to right.
Now from top to bottom, mark a number on paper at each side of the front and back. So there are 2×n×2k numbers in total and these numbers form a permutation P.
Now it expands to its original. These numbers from top to bottom, from front to back, from left to right form a permutation Q.
Given the permutation P, find the permutation Q.
See example for details.
For k=1 and P=1..4×n, you can assume that you are marking the page numbers before printing a booklet forming from n pieces of A4 papers.
Now from top to bottom, mark a number on paper at each side of the front and back. So there are 2×n×2k numbers in total and these numbers form a permutation P.
Now it expands to its original. These numbers from top to bottom, from front to back, from left to right form a permutation Q.
Given the permutation P, find the permutation Q.
See example for details.
For k=1 and P=1..4×n, you can assume that you are marking the page numbers before printing a booklet forming from n pieces of A4 papers.
输入格式
The first line contains a single integer T(1≤T≤30) , the number of test cases.
For each test case, the first line gives two integers n, k(1≤n≤200,1≤k≤10).
The next line gives the permutation P that consists of 2×n×2k integers pi(1≤pi≤2×n×2k).
It is guaranteed that ∑2×n×2k doesn't exceed 106.
For each test case, the first line gives two integers n, k(1≤n≤200,1≤k≤10).
The next line gives the permutation P that consists of 2×n×2k integers pi(1≤pi≤2×n×2k).
It is guaranteed that ∑2×n×2k doesn't exceed 106.
输出格式
The output should contain T lines each containing 2×n×2k integers separated by spaces, indicating the permutation Q.
输入样例 复制
1
2 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
输出样例 复制
12 5 4 13 11 6 3 14 10 7 2 15 9 8 1 16
数据范围与提示