7991: Balance Beam
题目描述

In order to save money for a new stall in her barn, Bessie the cow has started performing in the local circus, demonstrating her remarkable sense of balance as she carefully walks back and forth on an elevated balance beam!
The amount of money Bessie earns in her performance is related to where she manages to ultimately jump off the beam. The beam has positions labeled 0,1,…,N+10,1,…,N+1 from left to right. If Bessie ever reaches 00 or N+1N+1 she falls off one of the ends of the beam and sadly gets no payment.
If Bessie is at a given position kk, she can do either of the following:
1. Flip a coin. If she sees tails, she goes to position k−1k−1, and if she sees heads, she goes to position k+1k+1 (i.e. 1212 probability of either occurrence).
2. Jump off the beam and receive payment of f(k)f(k) (0≤f(k)≤109)(0≤f(k)≤109).
Bessie realizes that she may not be able to guarantee any particular payment outcome, since her movement is governed by random coin flips. However, ba
INPUT FORMAT (file balance.in):
The first line of input contains NN (2≤N≤1052≤N≤105). Each of the remaining NN lines contain f(1)…f(N)f(1)…f(N).
OUTPUT FORMAT (file balance.out):
Output NN lines. On line ii, print out 105105 times the expected value of payment if Bessie starts at position ii and plays optimally, rounded down to the nearest integer.
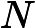



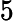

输入格式
2 1 3
输出格式
150000 300000
输入样例 复制
输出样例 复制