8946: Random
内存限制:128 MB
时间限制:1 S
题面:传统
评测方式:文本比较
上传者:
提交:0
通过:0
题目描述
Walk Alone has a strange random number generator, the pseudocode of which is as follows:
Now Walk Alone is given an array A and an integer k. He found that for any integer x (0≤x<2k), there exists a positive integer T such that randT(x,A)=x, where
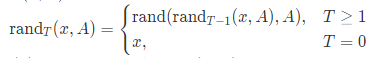
Let f(x)=min{T>0∣randT(x,A)=x}. Walk Alone wants to know the expected value of f(x) modulo 998244353998 if x is chosen from {0,1,…,2k−1} with equal probability.
It can be shown that the answer can always be expressed as an irreducible fraction x/y, where x and y are integers and y≢0(mod998244353). Output such an integer a that 0≤a<9982443530 ,0≤a<998244353 and a⋅y≡x(mod998244353).
uintk rand(uintk x, int A[]) {
for (int i = 0; i < n; ++i) {
if (A[i] >= 0) x ^= x << A[i];
else x ^= x >> -A[i];
}
return x;
}
Here 'uintk' denotes the type of unsigned integers with k binary bits, and 'n' denotes the size of array A. You can use 'std::bitset' in C++ to implement all operations involving 'uintk'.Now Walk Alone is given an array A and an integer k. He found that for any integer x (0≤x<2k), there exists a positive integer T such that randT(x,A)=x, where
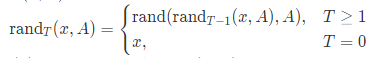
Let f(x)=min{T>0∣randT(x,A)=x}. Walk Alone wants to know the expected value of f(x) modulo 998244353998 if x is chosen from {0,1,…,2k−1} with equal probability.
It can be shown that the answer can always be expressed as an irreducible fraction x/y, where x and y are integers and y≢0(mod998244353). Output such an integer a that 0≤a<9982443530 ,0≤a<998244353 and a⋅y≡x(mod998244353).
输入格式
The first line contains two integers n (0≤n≤10^5) and k (1≤k≤32), the size of array A and the length of type 'uintk' respectively.
The second line contains n integers, the iii-th of which is Ai (0<∣Ai∣<k).
The second line contains n integers, the iii-th of which is Ai (0<∣Ai∣<k).
输出格式
Print the expected number of f(x) modulo 998244353998 in one line.
输入样例 复制
1 2
1输出样例 复制
499122178数据范围与提示
In the first example, when A=[1], the values of function rand and f are as follows:
rand(0,A)=0,f(0)=1.rand(1,A)=3,f(1)=2.
rand(2,A)=2,f(2)=1.
rand(3,A)=1,f(3)=2.
Hence the expected value of f is 1.5, which is congruent to 499122178 modulo 998244353.