8966: Counter Strike

SPY likes useful algorithms, while Markyyz always learns useless algorithms. Although they learn different type of algorithms, they both like a computer game called Counter Strike ("$CS$" for short, different from the game with the same name in reality). It is a two-player competition. One player acts as a terrorist ("$T$" for short), responsible for planting bombs. The other one acts as a counter terrorist ("$CT$" for short), responsible for defusing bombs.

At the start of each game, the system generates a bomb with a circuit in it. The circuit consists of $n$ hubs (numbered from $1$ to $n$) and $m$ wires. Each wire connects two different hubs, any two hubs could be directly or indirectly connected by wires, and no two hubs are directly connected by more than one wire. In other word, the circuit can be regarded as an undirected graph with $n$ vertices and $m$ edges, without multiple-edges or self-loops.

The game is divided into three stages:

1. Bomb planting stage: $T$ will receive $k$ activating components numbered from $1$ to $k$. $T$ needs to select $k$ different hubs ℎ1,ℎ2,...,ℎ�h1,h2,...,hk, and set the $i$-th activating component on the ℎ�hi-th hub.
2. Bomb defusing stage: $CT$ will receive a useful kit for free, and buy $q$ useless kits numbered from $1$ to $q$. A useful kit can remove an arbitrary hub, while a useless kit can only remove a hub with an activating component in order, which means the $i$-th useless kit can only remove the ℎ�hi-th hub. Once a hub is removed, all wires directly connected to it will be cut off.
3. Bomb activating stage: If any two activating components are connected directly or indirectly by wires, the bomb will be activated and $T$ will win. Otherwise, the bomb will be defused and $CT$ will win.

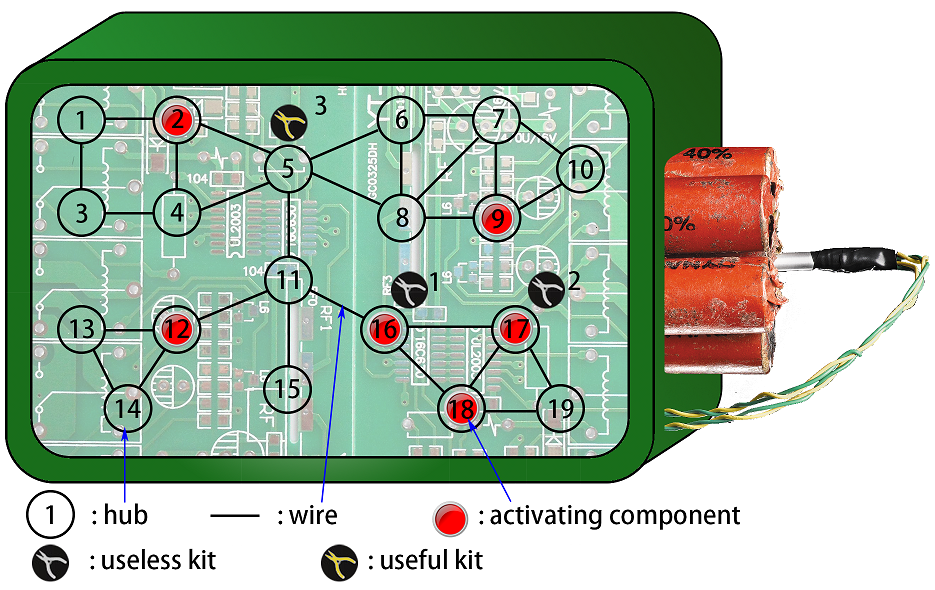
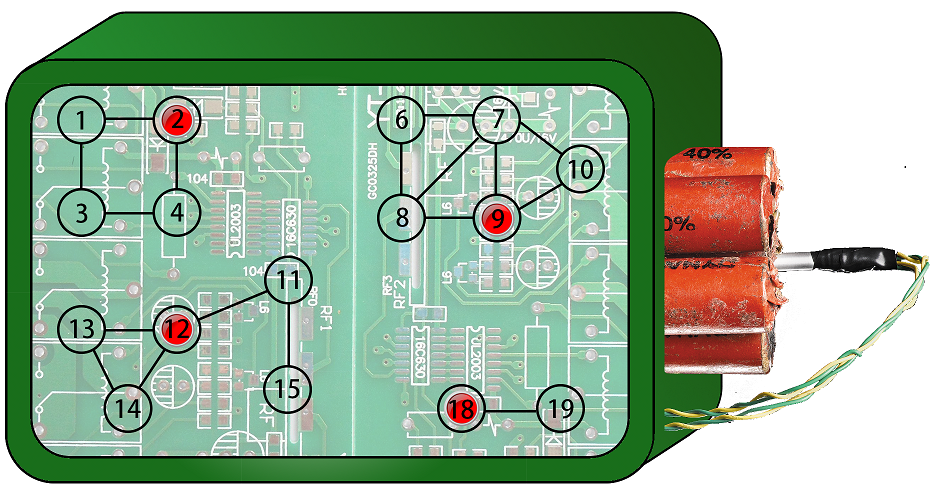
For example, the picture above shows a bomb with a circuit consisting of $19$ hubs and $27$ wires. $T$ obtained $6$ activating components and set them on hub $16,17,2,18,12,9$. $CT$ can buy $2$ useless kits to remove the $16$-th and the $17$-th hub, then remove the $5$-th hub with a useful kit.

Now Markyyz acts as $T$, and SPY acts as $CT$. Markyyz has placed $k$ activating components. To save money for the future games, SPY wants to buy the minimum number of useless kits to defuse the bomb. Although SPY makes himself master of useful algorithms, he can't find the answer within the time complexity of $O((n+m)\log n)$. Can you help him to calculate the answer (in other word, the minimum value of $q$ for $CT$ to win the game) ?

The first line of the input contains an integer $t$ $(1\le t\le 5000)$, indicating the number of test cases.

In each test case:

The first line contains three integers $n,m,k$ (2≤�,�≤2×105,2≤�≤�)(2≤n,m≤2×105,2≤k≤n), indicating the number of hubs, the number of wires, and the number of activating components.

The next $m$ lines, each line contains two integers $u,v$ $(1\le u,v\le n,u\ne v)$, indicating a wire connected to the $u$-th hub and the $v$-th hub.

The next line contains $k$ different integers ℎ1,ℎ2,...,ℎ�h1,h2,...,hk (1≤ℎ�≤�)(1≤hi≤n). The $i$-th activating component is set in the ℎ�hi-th hub.

It is guaranteed that in all test cases ∑�,∑�≤106∑n,∑m≤106.