P8974 - SPY finding NPY

内存限制：64 MB 时间限制：1 S

题面：传统评测方式：文本比较上传者：

提交：0 通过：0

Recently, SPY has retired from XCPC. He cherishes the memory of learning algorithms from scratch and winning the ICPC gold medal. So he is finding an NPY (non-programming youth) to be his successor. SPY is so popular that $n$ NPYs want to be his apprentice. As SPY only needs one NPY, he sets a test for the $n$ NPYs. The rules are as follows:

$n$ NPYs are indexed from $1$ to $n$ . SPY will interview the $n$ NPYs in order. The $i$ -th NPY will be tested in the $i$ -th interview. After an NPY is interviewed, SPY will get her IQ (intelligence quotient) number (an integer in $[0, 202 3^{202 3^{2023}}]$ ) . SPY can decide whether to accept her or not. Once he accepts an NPY, the test would be finished and he won't interview the following NPYs. Once he refuses an NPY, he won't give her another chance.

Notice that there are no two NPYs with the same IQ. SPY has a specital strategy to find an NPY with high IQ. He sets an integer $k$ $(0 \leq k < n)$ before the test.

1、No matter how intelligent the first $k$ NPYs are, they will be refused. SPY will record the highest IQ number $x$ within the first $k$ NPYs. If $k = 0$ then $x = - 1$ .

2、Then he will interview the $(k + 1)$ -th to the $(n - 1)$ -th NPY. Once SPY interviews an NPY with IQ higher than $x$ , he will accept her and finish the test.

3、If no NPY is accepted, SPY will accept the $n$ -th NPY.

The IQ rank of the $n$ NPYs is random, which means their rank is a permutation of $1 \sim n$ , and the $n!$ possible situations occur with equal probability. Althouth SPY is a master of useful algorithms, it is difficult for him to set the number $k$ . Can you help him to calculate the minimum $k$ to maximize the probability to accept the NPY with the highest IQ?

The first line contains a single integer $T$ $(1 \leq T \leq 1 0^{4})$ , indicating the number of test cases.

The next $T$ lines, each line contains a single integer $n$ $(1 \leq n \leq 1 0^{4})$ , indicating the number of NPYs.

For each test, you should output one integer in a line, indicating the integer

k

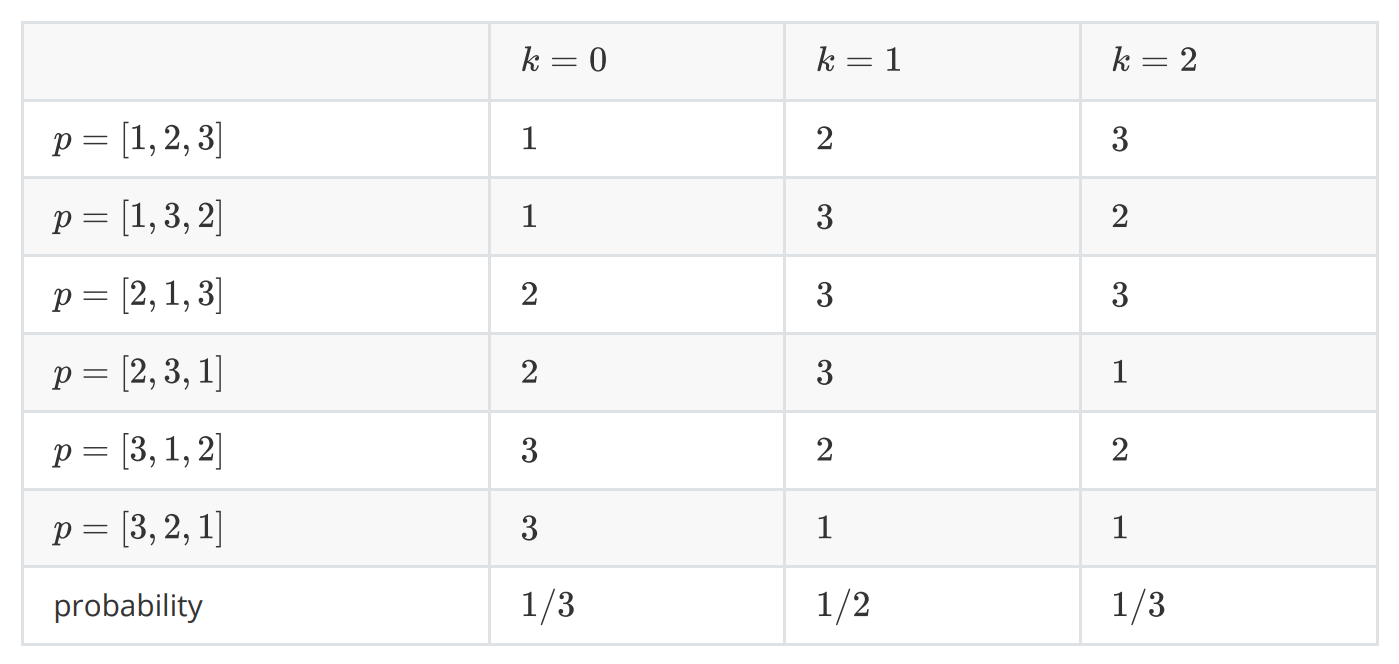
In the third test, there are $3$ NPYs. Let the array $p$ represent to the IQ rank. The IQ rank of $i$ -th NPY is $p_{i}$ . The $u$ -th NPY with $p_{u} = 1$ has the lowest IQ, and the $v$ -th NPY with $p_{v} = 3$ has the highest IQ.

There are $3! = 6$ situations occur with equal probability. The following list shows the IQ rank of the accepted NPY in all situations, and the probability to accept the NPY with the highest IQ.

2023杭电多校2

8974: SPY finding NPY

题目描述

输入格式

输出格式

输入样例复制

输出样例复制

数据范围与提示

分类标签