9106: Clamped Sequence II
内存限制:512 MB
时间限制:5 S
题面:传统
评测方式:Special Judge
上传者:
提交:1
通过:1
题目描述
链接:https://ac.nowcoder.com/acm/contest/57362/C
来源:牛客网
For an integer sequence a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an and a positive integer ddd, the ddd-clamped value of the sequence is the maximum value of ∑i=1n−1∑j=i+1n∣ai−aj∣\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}|a_i - a_j|∑i=1n−1∑j=i+1n∣ai−aj∣, where ∣x∣|x|∣x∣ is the absolute value of xxx, after appointing a range [l,r][l,r][l,r] satisfying 0≤r−l≤d0 \le r-l \le d0≤r−l≤d and clamping the sequence to the range [l,r][l, r][l,r].
More specifically, clamping the sequence to the range [l,r][l,r][l,r] makes each element
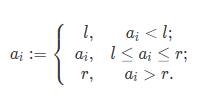

Both lll and rrr are arbitrary real numbers decided by you under the given constraints. It can be shown that the maximum sum is always an integer.
Now, given an integer sequence a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an and qqq queries, where each query is in one of the two following formats:
Please output the answer for each reporting queries.
来源:牛客网
For an integer sequence a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an and a positive integer ddd, the ddd-clamped value of the sequence is the maximum value of ∑i=1n−1∑j=i+1n∣ai−aj∣\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}|a_i - a_j|∑i=1n−1∑j=i+1n∣ai−aj∣, where ∣x∣|x|∣x∣ is the absolute value of xxx, after appointing a range [l,r][l,r][l,r] satisfying 0≤r−l≤d0 \le r-l \le d0≤r−l≤d and clamping the sequence to the range [l,r][l, r][l,r].
More specifically, clamping the sequence to the range [l,r][l,r][l,r] makes each element
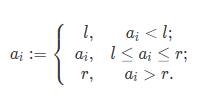
Both lll and rrr are arbitrary real numbers decided by you under the given constraints. It can be shown that the maximum sum is always an integer.
Now, given an integer sequence a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an and qqq queries, where each query is in one of the two following formats:
- 111 xxx ddd denotes setting axa_xax to ddd
- 222 ddd denotes reporting the d-clamped value of the current sequence
Please output the answer for each reporting queries.
输入格式
The first line contains two integers nnn (2≤n≤1052\le n\le 10^52≤n≤105) and qqq (1≤q≤1051\le q\le 10^51≤q≤105), denoting the length of the given sequence and the number of queries.
The second line contains nnn integers a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an (1≤ai≤1061 \le a_i \le 10^61≤ai≤106), denoting the given sequence.
Each of the following qqq lines contains a query, which is in one of the two following formats:
111 xxx ddd (1≤x≤n1 \le x \le n1≤x≤n, 1≤d≤1061 \le d \le 10^61≤d≤106) denotes setting axa_xax to ddd
222 ddd (1≤d≤1061 \le d \le 10^61≤d≤106) denotes reporting the ddd-clamped value of current sequence
The second line contains nnn integers a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an (1≤ai≤1061 \le a_i \le 10^61≤ai≤106), denoting the given sequence.
Each of the following qqq lines contains a query, which is in one of the two following formats:
111 xxx ddd (1≤x≤n1 \le x \le n1≤x≤n, 1≤d≤1061 \le d \le 10^61≤d≤106) denotes setting axa_xax to ddd
222 ddd (1≤d≤1061 \le d \le 10^61≤d≤106) denotes reporting the ddd-clamped value of current sequence
输出格式
For each reporting query, output one line containing a single integer, denoting the ddd-clamped value of the current sequence.
输入样例 复制
8 3
3 1 4 1 5 9 2 6
2 3
1 2 8
2 4输出样例 复制
46
58