9131: Peek
内存限制:256 MB
时间限制:1 S
题面:传统
评测方式:文本比较
上传者:
提交:2
通过:1
题目描述
There is a large cave with words written on its inner wall, and Bob wants to see these words. Unfortunately, the interior of the cave has a large number of traps, thus making it difficult to enter; fortunately, the cave has been opened up with many windows at the corners, through which one can peek at the texts.
In the process of looking in through a particular window, the edge of the polygon might be parallel to the line of sight, and then it would be difficult to see the writing on the inner wall. At this moment, you can make the inner wall no longer parallel to the line of sight, by making small movements by the window.
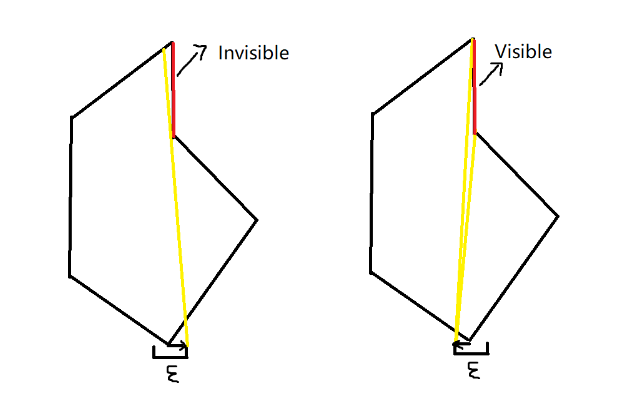
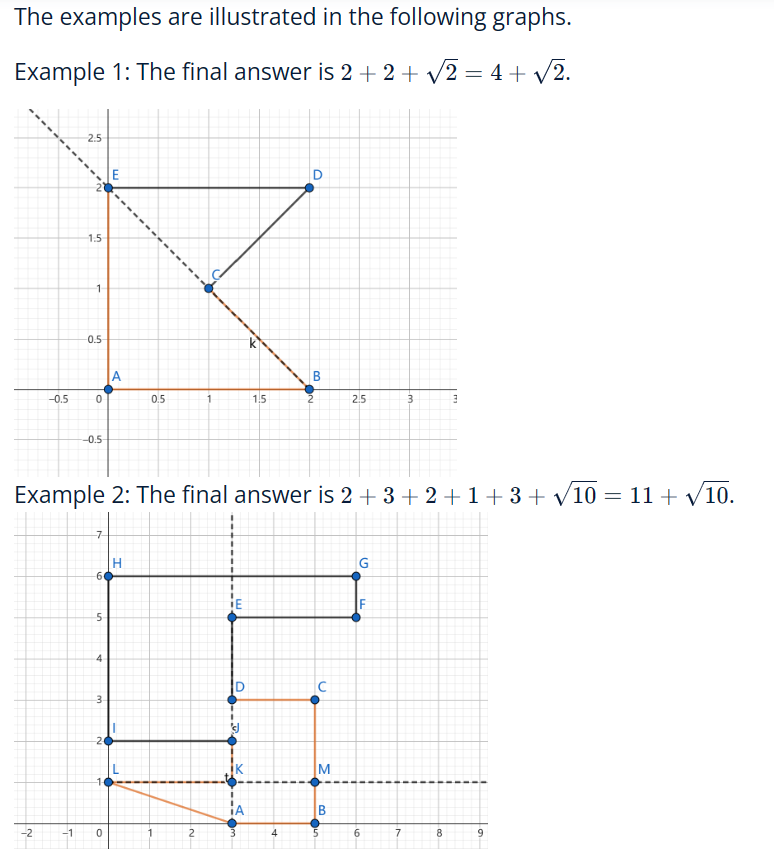
Formally, The large cave can be viewed as a polygon P which doesn't intersect with itself, with many of its vertices {Pi} serving as windows. When observing from the outer area of a polygon into a vertice A serving as a window, the observer's line of sight will be restricted by two edges adjacent to A, which is shown in the following graph. Segments observable from A will contribute to the total length of the answer. In addition, the observer can make a tiny movement ε parallel to the window, thus making some of the edge observable.
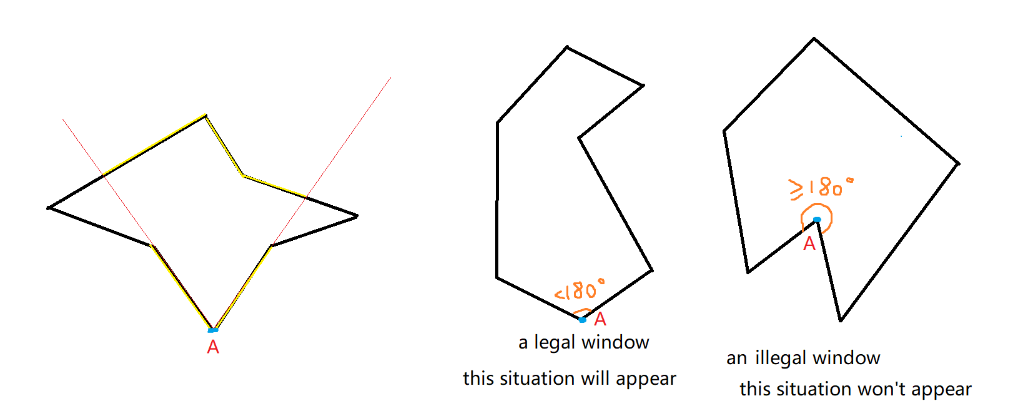
It is guaranteed that the point which is chosen as a window will form an angle α ≤ 180◦ with its two adjacent edges.
Now, Bob wants to know what is the total inner wall length that can be seen by peering through all the windows. Please note that ε can be seen as a very small number, and it multiplied with any constant k won't make contribute to the final answer.
In the process of looking in through a particular window, the edge of the polygon might be parallel to the line of sight, and then it would be difficult to see the writing on the inner wall. At this moment, you can make the inner wall no longer parallel to the line of sight, by making small movements by the window.

Formally, The large cave can be viewed as a polygon P which doesn't intersect with itself, with many of its vertices {Pi} serving as windows. When observing from the outer area of a polygon into a vertice A serving as a window, the observer's line of sight will be restricted by two edges adjacent to A, which is shown in the following graph. Segments observable from A will contribute to the total length of the answer. In addition, the observer can make a tiny movement ε parallel to the window, thus making some of the edge observable.

It is guaranteed that the point which is chosen as a window will form an angle α ≤ 180◦ with its two adjacent edges.
Now, Bob wants to know what is the total inner wall length that can be seen by peering through all the windows. Please note that ε can be seen as a very small number, and it multiplied with any constant k won't make contribute to the final answer.
输入格式
The first line consists of an integer T(1 ≤ T ≤ 10), denoting the number of test cases.
In each test case, the first line gives two integers n(1 ≤ n ≤ 100), m(1 ≤ m ≤ n), indicating the number of vertices of the polygon and the number of windows.
The next section consists of n lines, each line giving two integers x(−109 ≤ x ≤ 109),y(−109 ≤ y ≤ 109), indicating the coordinates of the corresponding points.
The next m line gives m integers, indicating the subscripts of windows.
It is guaranteed that the two adjacent points will have adjacent subscripts. For example, if point A and point B are adjacent in the polygon, and A is P 2, then B will be P1 or P3.
In each test case, the first line gives two integers n(1 ≤ n ≤ 100), m(1 ≤ m ≤ n), indicating the number of vertices of the polygon and the number of windows.
The next section consists of n lines, each line giving two integers x(−109 ≤ x ≤ 109),y(−109 ≤ y ≤ 109), indicating the coordinates of the corresponding points.
The next m line gives m integers, indicating the subsc
It is guaranteed that the two adjacent points will have adjacent subsc
输出格式
Outputs one float number with 3 decimal places, representing the total length that can be seen.
输入样例 复制
2
5 1
0 0
2 0
1 1
2 2
0 2
2
12 2
3 0
5 0
5 3
3 3
3 5
6 5
6 6
0 6
0 2
3 2
3 1
0 1
1
12输出样例 复制
5.414
14.162数据范围与提示